Confidence set
ブートストラップを用いた,単回帰における信頼集合の可視化
Introduction
サブタイトルにある通り,ブートストラップを用いて単回帰における信頼集合を可視化する.コレが本記事の目標である.
具体的には,
1. データの生成
2. ブートストラップでOLSEをたくさんgetする
3. 横軸を定数項,縦軸を回帰係数にしてplotする
4. plotした散布図に楕円を描くである
また,大した意味はないが,それぞれのプロセスで異なるプログラミング言語を使用する.
1 データの生成 (R)
Rでデータを生成しよう.サンプルサイズは1000.説明変数は1つで単回帰である.
まず,真のパラメータの値を設定する
alpha <- 1.2
beta <- 1.8次に,説明変数と応答変数を生成しよう.
X <- rnorm(n = 1000, mean = 10, sd = 5)
mu <- alpha + beta * X
Y <- rnorm(n = 1000, mean = mu, sd = 2)ちなみに,muのように,応答変数のパラメータの構造を記述している部分を線形予測子と呼ぶ.
ベイジアン出ない限りそこはどうでもいい.
最後に,生成したデータをcsvに書き出そう.
myd <- cbind(X,Y)
write.csv(myd, file = "myd.csv",row.names = FALSE)2 ブートストラップ (Julia)
ブートストラップの説明は“計量経済学|日本評論社” (n.d.)に詳しい.
ブートストラップは復元抽出を何度も繰り返すので,時間がかかる.そこでJuliaの出番である.
とりあえず,必要なパッケージと,さっき書き出したcsvを読み込もう
using CSV, DataFrames, LinearAlgebra
df = CSV.read("myd.csv", DataFrame)いきなりブートストラップをする前に,juliaでの単回帰の実装例を提示する.
#計画行列の定義
X = hcat(ones(1000), df.X)
#応答変数の定義
Y = df.Y
#OLSEの行列表記
beta = X'X \ X'Y以上である.
上記のOLSをたくさん繰り返そう.具体的には,B=5000!
row_idx = rand(1:1000)で1から1000までの数字をランダムに生成し,その数字をindexとして行を選ぶ.選ばれた行を別のmatrixに上から順番に代入していく.これで復元抽出ができているハズ.
復元抽出されたdataでOLSを回して,OLSEをゲットする.これを5000回繰り返す.
data = similar(df, 1000)
result = zeros(5000,2)
for b in 1:5000
for k in 1:1000
row_idx = rand(1:1000)
data[k, :] = df[row_idx, :]
end
X = hcat(ones(1000), data.X)
Y = data.Y
beta = (X'X) \ (X'Y)
result[b,:] = beta
end定数項と回帰係数のペアが5000組生成できたので,コレをまたcsvに保存しよう.
CSV.write("result.csv", Tables.table(result))3 可視化
可視化にはpythonを用いる.
一旦,普通にcsvを読み込んで,可視化してみよう
まずはライブラリのインポート
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as LAcsvの読み込みと可視化
df = pd.read_csv("result.csv")
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(df["Column1"], df["Column2"], s=10, alpha=0.5)
ax.set_xlabel("Intercept")
ax.set_ylabel("Slope")
ax.set_title("Bootstrap OLS estimates")
plt.show()出力結果は Figure 1 である
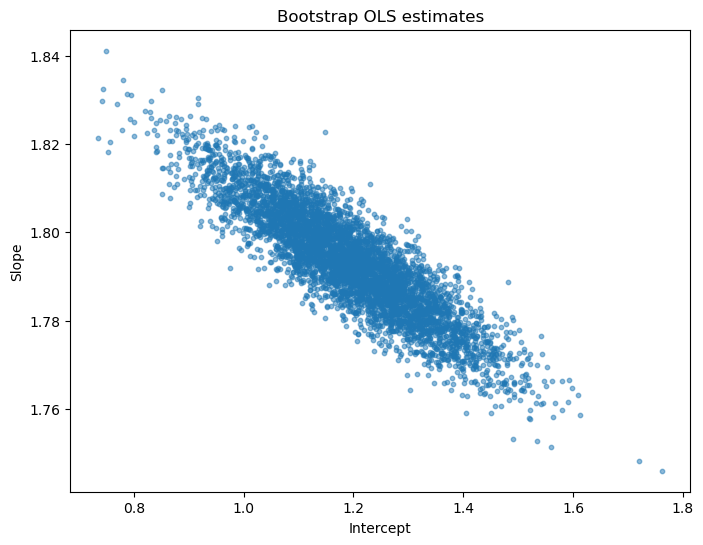
4 楕円の上書き
本記事の最終目標は,この散布図に95%のデータを内包するような楕円を描くことである.
ざっくりとした方針としては,まず単位円を考え,これをいい感じに拡大(縮小)し,いい感じに縦横比率を変形させ,いい感じに回転させれば,いい感じの楕円が描けそうである.
具体的には,定数項と回帰係数は漸近正規性があるので,Figure 1 を,2変量正規分布からのデータ生成とみなし,平均ベクトルと分散共分散行列の情報を使う.
“多変量正規分布の確率等高線の書き方(2/4)” (2023)と“多変量正規分布の確率等高線の書き方(3/4)” (2023)を参考にした.
では,楕円を上書きしていこう.
平均ベクトルと分散共分散行列を計算する.
#平均ベクトル
mu = df[["Column1","Column2"]].to_numpy().mean(axis=0).reshape(2, 1)
#分散共分散行列
sig = np.cov(df[["Column1","Column2"]].to_numpy(), rowvar=False)分散共分散行列を固有値分解する.固有値分解によって得られた新たな行列が,単位円を楕円に変換するのに必要なのである.
l,p = LA.eig(sig)
print("固有値")
print(l) # 固有値
print("固有ベクトル P ")
print(p) # 固有ベクトル(正規化済)対角行列D,D^(1/2),Pの逆行列を定義
d = np.diag(l)
sqrtd = np.diag(np.sqrt(l))
pinv = LA.inv(p)うまく分解できていれば,元の行列が復元できるハズ.みてみよう
print(sig)
print(np.dot(np.dot(p,d),pinv))単位円の座標を考え,いい感じの楕円になるように座標を変換していく.座標の変換プロセスで,固有値分解で得られる行列が必要だった.
n = 200 #角度を200に分割する
t = np.arange(0, 2*np.pi, 2*np.pi/n) # 媒介変数
xy = np.array( [np.cos(t), np.sin(t)] ) #単位円の作成
xy2 = mu + np.sqrt(5.991) * (p @ sqrtd @ xy) #単位円の変換散布図と楕円の可視化
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(xy2[0], xy2[1], c="red")
ax.scatter(df["Column1"], df["Column2"], s=10, alpha=0.5)
ax.set_xlabel("Intercept")
ax.set_ylabel("Slope")
ax.set_title("Bootstrap OLS estimates")
plt.show()出力結果は Figure 2 である
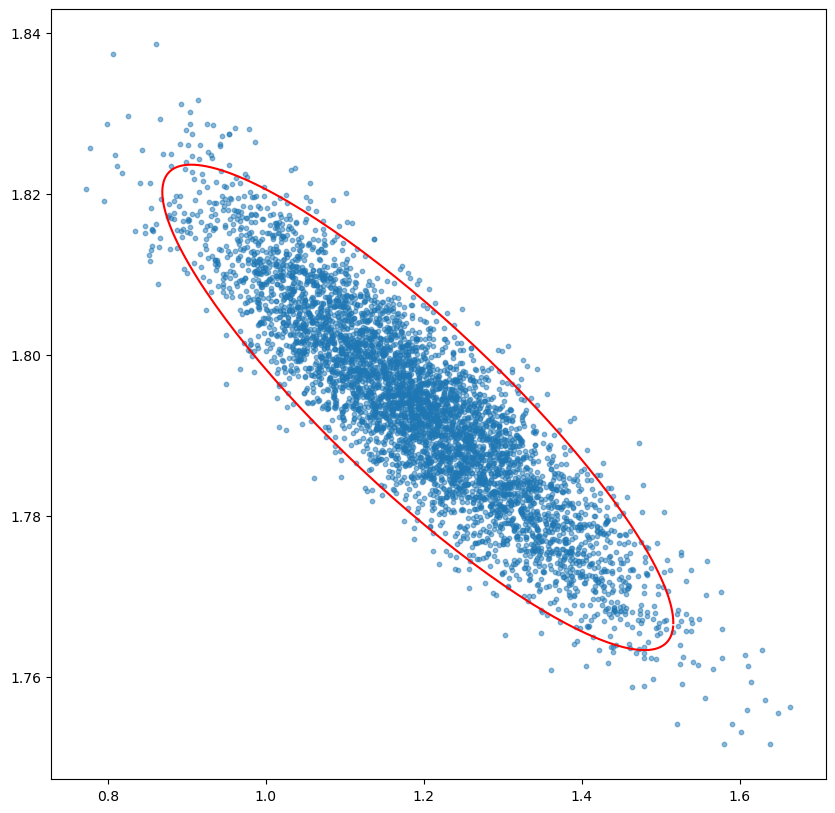
信頼集合という考え方は,信頼区間を2次元に拡張したものであり,知っておいても損はしない(おそらく得もしないが).“部分識別入門|日本評論社” (n.d.)では,バウンドの信頼集合を考えたりしているので,anti点識別の方はそちらもどうぞ.